Introduction to Data Structures, Algorithms, and Acing Coding Interviews 🕴️

Name	Link	Created By	Accepted By	Actions

Welcome to the next step in your journey as a budding software developer. Having gained a solid foundation in Ruby and full-stack web development with Rails, you’re now poised to delve deeper into the world of data structures and algorithms. This module is designed to arm you with the tools and knowledge necessary to excel in technical interviews and solve complex problems efficiently. Let’s embark on this adventure together, where you will not only sharpen your coding skills but also become adept at thinking critically about algorithmic challenges.

Here is a video for this lesson

Time and Space Complexity

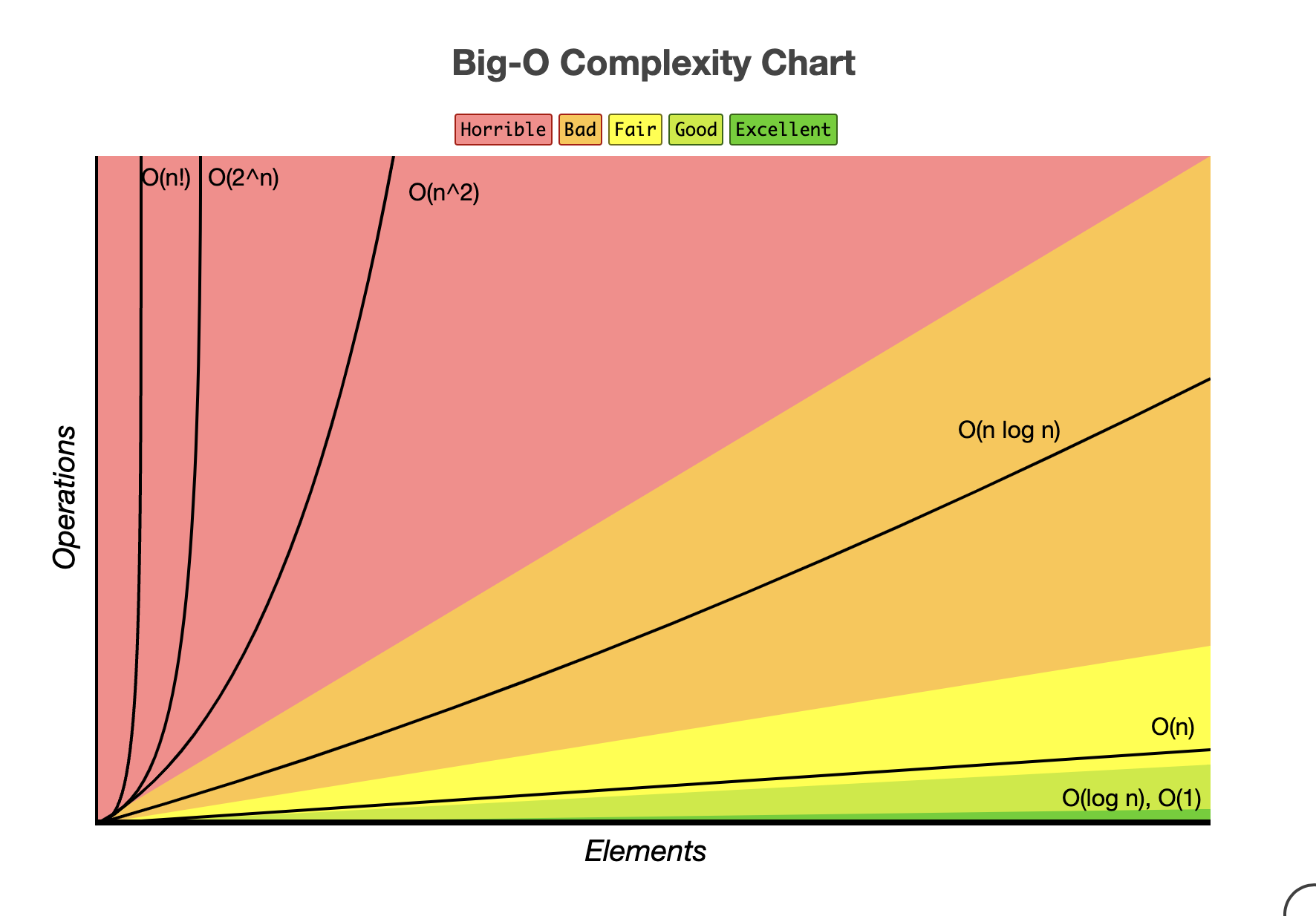
Embracing Big O Notation: The Gateway to Efficiency 📈

Before we dive into specific data structures and algorithms, let’s talk about Big O Notation. Big O Notation is a mathematical notation that describes the complexity of your algorithm in terms of time and space. It’s a crucial concept for understanding how well an algorithm scales as the size of the input data increases. Think of it as a way to quantify the efficiency of your solution, helping you to identify whether you’re truly inventing the most effective approach to a problem.

source

Let’s dive into some example code snippets in Ruby, illustrating common data structures and algorithms along with their associated Big O notations. These examples will help you understand how these concepts apply in real-world coding scenarios, particularly in the context of technical interviews.

Examples

Iterating over an Array

Time Complexity: O(n) - This is because each element in the array is visited exactly once, so the time it takes to complete this operation scales linearly with the size of the array.

Space Complexity: O(1) - The space required is constant since we’re only printing the elements without storing anything extra.

Nested Loop

Consider a scenario where we want to find all possible pairs of elements within an array. This task can be accomplished using a nested loop, where the outer loop iterates through each element, and the inner loop iterates through the elements again to pair with the element selected by the outer loop.

Time Complexity: O(n^2) - This is because for each element in the array, the inner loop runs nearly n times, leading to a total of approximately n * n iterations. The time complexity scales quadratically with the size of the array, making it less efficient for large datasets.

Space Complexity: O(1) - The space required is constant since we’re only printing the pairs without storing any additional structures that grow with the input size.

Hash Lookup

Time Complexity: O(1) - Looking up a value in a hash by its key is a constant-time operation, meaning it takes the same amount of time regardless of the size of the hash.

Space Complexity: O(1) - The space complexity is constant with respect to the number of key-value pairs stored in the hash.

Binary Search

Binary search is a fast algorithm for finding the position of a value within a sorted array. It works by repeatedly dividing in half the portion of the list that could contain the value, until you’ve narrowed the possible locations to just one.

Binary Search

# Define a method for performing binary search that returns the index of the value in the array (or nil if it doesn't exist)
# array: The sorted array in which to search for the value
# value: The value to search for
# from: The starting index of the segment of the array to be searched
# to: The ending index of the segment of the array to be searched
def binary_search(array, value, from=0, to=nil)
  # Set the default search range to the entire array if 'to' is not specified
  to = array.count - 1 unless to

# Calculate the middle index of the search range
  mid = (from + to) / 2

# If the search value is less than the middle value, search the left half
  if value < array[mid]
    return binary_search(array, value, from, mid - 1)
  # If the search value is greater than the middle value, search the right half
  elsif value > array[mid]
    return binary_search(array, value, mid + 1, to)
  # If the search value matches the middle value, return the middle index
  else
    return mid
  end
end

sorted_numbers = [1, 4, 7, 9, 15, 24, 30]
puts binary_search(sorted_numbers, 15)

Time Complexity: O(log n) - Binary search has a logarithmic time complexity because it splits the search interval in half each time, significantly reducing the number of comparisons needed to find the target value.

Space Complexity: O(log n) due to the call stack, which uses space proportional to the depth of the recursion, which is logarithmic.

Bubble Sort

The bubble sort algorithm is a simple sorting algorithm that repeatedly steps through the array, compares adjacent elements, and swaps them if they are in the wrong order. The pass through the array is repeated until the list is sorted. The algorithm is named for the way smaller elements “bubble” to the top of the array (beginning of the array) because they are lighter, while larger elements sink to the bottom (end of the array).

Bubble Sort

# Define a method named bubble_sort that takes an array as its parameter
def bubble_sort(array)
  # Get the number of elements in the array
  n = array.length
  
  # Start an infinite loop that will be broken explicitly when no swap is needed
  loop do
    # Initialize swapped to false on each new iteration of the loop
    swapped = false

# Iterate over the array from 0 to n-2 (inclusive) using |i| as the index
    (n-1).times do |i|
      # If the current element is greater than the next element
      if array[i] > array[i+1]
        # Swap the elements. This is the "bubble" part of the sorting
        
        # Store the value of the current element in a temporary variable
        temp = array[i]
        # Assign the next element's value to the current element
        array[i] = array[i+1]
        # Assign the stored value from the temporary variable to the next element
        array[i+1] = temp

# Mark that a swap has occurred
        swapped = true
      end
    end

# If no elements were swapped in the last iteration, the array is sorted
    break unless swapped
  end
  # Return the sorted array
  array
end

# Create an array of unsorted numbers
unsorted_numbers = [4, 2, 7, 1, 3]
# Call the bubble_sort method with the unsorted array and print the sorted array
puts bubble_sort(unsorted_numbers)

Time Complexity: O(n^2) - Bubble sort is an example of a quadratic time complexity algorithm because it involves nested iterations over the collection, making it less efficient for large datasets.

Space Complexity: O(1) - Bubble sort sorts the array in place and does not require additional storage that grows with the input size, making its space complexity constant.

Recursive Fibonacci

The Fibonacci sequence is a series of numbers where each number is the sum of the two preceding ones, usually starting with 0 and 1. That is, the sequence goes 0, 1, 1, 2, 3, 5, 8, 13, and so forth. The sequence is named after Leonardo of Pisa, known as Fibonacci, who introduced it to the Western world with his 1202 book “Liber Abaci”.

In the context of programming, the Fibonacci sequence can be generated using various methods, including iterative loops and recursion. The example provided uses recursion, which is a method where the solution to a problem depends on solutions to smaller instances of the same problem.

Recursive Fibonacci

Time Complexity: O(2^n) - The time complexity of the recursive Fibonacci algorithm is exponential due to the fact that it generates an exponentially growing number of function calls.

Space Complexity: O(n) - The space complexity of the recursive Fibonacci is linear in the worst case due to the call stack. For each function call, a new frame is added to the call stack, and in the worst case, there are ‘n’ recursive calls for computing fibonacci(n).

Data Structures: The Building Blocks 🧱

Data structures are foundational concepts that enable us to organize and store data in a way that facilitates efficient access and modification. Here are some of the key structures you’ll learn about:

Arrays: Store a list of items in a specific order.
Hashes: Also known as dictionaries in other languages, hashes map keys to values, enabling fast retrieval based on a key.
Linked Lists: A collection of nodes that together form a sequence. Each node contains data and a reference to the next node in the sequence.
Trees: Hierarchical data structures that consist of nodes in a parent/child relationship.
Graphs: Collections of nodes (vertices) connected by edges. Useful for modeling networks like social connections or maps.

Understanding these structures is paramount as they form the basis of more complex algorithms and problem-solving techniques.

Algorithms: The Logic Behind the Magic 🧙‍♂️

An algorithm is a step-by-step procedure for performing a task or solving a problem, like a recipe or step-by-step instructions. Mastering algorithms means understanding a set of core principles that can be applied to a wide range of challenges. We’ll learn about:

Sorting Algorithms: Such as bubble sort, selection sort, and more efficient ones like quicksort and mergesort.
Search Algorithms: Including linear search and binary search, understanding their differences in complexity.
Recursive Algorithms: Techniques that solve problems by solving smaller instances of the same problem.
Dynamic Programming: A method for solving complex problems by breaking them down into simpler subproblems.

Acing the Coding Interview: Strategies and Mindset 🤔

The coding interview is your opportunity to showcase your problem-solving skills, logical thinking, and mastery of data structures and algorithms. Here are some tips to help you prepare:

Practice, Practice, Practice: There’s no substitute for hands-on problem-solving. Use platforms like LeetCode, HackerRank, and others to hone your skills.
Understand the Problem: Before jumping into code, make sure you fully understand what’s being asked. Clarify any doubts with your interviewer.
Think Aloud: Interviewers want to see how you approach problems. Verbalize your thought process and write pseudocode as you break down the problem and explore solutions.
Start with a Brute Force Solution: It’s okay to start with a simpler, less efficient solution. You can always refine it later.
Test Your Code: Before declaring that you’re done, test your solution with different inputs to ensure it handles edge cases.

Pro Tips

Setup Your Local Environment

Create a repository for all your data structures and algorithms practice. You can use the Data Structures and Algorithms Workspace template to get started. This setup allows you to track your progress as you work through each problem.

Write Unit Tests with MiniTest

MiniTest is a unit testing framework included with Ruby. Writing tests helps ensure your solutions are correct and robust.

For example, if you have a fibonacci.rb file:

      # ./fibonacci.rb

def fibonacci(n)
  return n if n <= 1

  fibonacci(n-1) + fibonacci(n-2)
end

You can create a MiniTest file at tests/test_fibonacci.rb to test your code:

      # ./tests/test_fibonacci.rb
require 'minitest/autorun'
require_relative '../fibonacci'

class TestFibonacci < Minitest::Test
  def test_fibonacci_zero
    assert_equal 0, fibonacci(0)
  end

  def test_fibonacci_five
    assert_equal 5, fibonacci(5)
  end

  def test_fibonacci_ten
    assert_equal 55, fibonacci(10)
  end
end

    

Run the tests with:

      ruby tests/test_fibonacci.rb

    

Practicing Test Driven Development (TDD), where you write tests before the implementation, can be highly beneficial.

Use a Debugger

The debug gem adds debugging functionality like breakpoints. To use it, first create a Gemfile with bundle init, then add the debug gem:

      # Gemfile

gem "debug"

Use the debugger in your code:

      # ./fibonacci.rb

require 'debug'

def fibonacci(n)
  debugger # breakpoint
  return n if n <= 1

  fibonacci(n-1) + fibonacci(n-2)
end

Running your code will pause execution at the breakpoint, allowing you to step through and inspect variables:

      ruby fibonacci.rb

    

      [1, 10] in fibonacci.rb
     1| 
     2| require 'debug'
     3| 
     4| def fibonacci(n)
=>   5|   debugger # breakpoint
     6|   return n if n <= 1
     7| 
     8|   fibonacci(n-1) + fibonacci(n-2)
     9| end
    10| 
=>#0    Object#fibonacci(n=5) at fibonacci.rb:5
  #1    <main> at fibonacci.rb:11
(rdbg)

    

Emulating the Inventor Mindset 💡

As you progress through this module, remember the ethos of being an inventor. Just as you’ve learned to creatively combine Ruby’s building blocks to solve problems, you’ll now apply a similar mindset to algorithmic challenges. Approach each problem with curiosity, leveraging your understanding of data structures and algorithms to devise innovative solutions.

This module is not just about preparing you for job interviews; it’s about cultivating a deeper understanding of computer science principles that will make you a better developer. As you complete the exercises and projects ahead, keep the lessons from your Ruby journey close at hand. They’re not just stepping stones but foundational elements of the inventive solutions you’ll create.

Good luck, and remember to ask questions, experiment, and, most importantly, enjoy the process of learning and discovery.

Assessment Details

Review your overall progress for this lesson

Assessment Title	Earned Points	Current Progress	Assessment Points
Iterating over an Array	0.0	0%	1
Finding All Pairs in an Array	0.0	0%	1
Hash Lookup	0.0	0%	1
Binary Search	0.0	0%	1
Bubble Sort	0.0	0%	1
Recursive Fibonacci	0.0	0%	1
Searching an Unsorted Array	0.0	0%	1
Hash Table Insertion	0.0	0%	1
Accessing an Element in a Linked List	0.0	0%	1
Merging Sorted Arrays	0.0	0%	1
Totals	0	0%	10

Earned Points

0/10

No highlights created for this lesson

Create a highlight by selecting any text in this lesson, and ask a question about it.

Create Invitation Link

Assessment Details

Review your overall progress for this lesson

No highlights created for this lesson